| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- pytorch
- ai_캠프
- conda
- chromeextention
- djangorestframework
- finpilot
- Github
- aws
- django
- ai캠프
- ML
- 오블완
- streamlit
- 로컬 런타임
- 정치기 필기
- Python
- 파이썬
- team_project
- seaborn
- pandas
- ai 캠프
- Jupyterlab
- 머신러닝
- sLLM
- lightsail
- EC2
- ollama
- mifare
- 티스토리챌린지
- mysql
- Today
- Total
greatsangho의 이야기
캠프 19일차 - 머신러닝(선형회귀) 본문
머신러닝은 학습하는 데이터의 정답의 유무에 따라 각각 지도학습과 비지도 학습으로 나뉜다.
지도 학습(supervised learning)은 대표적으로 회귀분석, 분류가 있고,
비지도 학습(unsupervised learning)은 대표적으로 군집 분석이 있다.
머신러닝을 진행하는 과정은
데이터 수집 --> 데이터 정리(전처리) --> 데이터 분리(훈련/검증) --> 알고리즘 선택 --> 모형 학습(훈련) --> 예측(검증) --> 모형 평가 --> 모형 활용의 단계를 거치게 된다.
지도학습에서 회귀분석은 값을 예측하는 분석 방법으로 값을 나누는 분류와 차이가 있다.
회귀분석은 여러개의 독립변수 x를 머신러닝 알고리즘을 거쳐 종속변수 y를 계산하는 과정이다.
방정식의 해를 구하는 과정이라 생각하면 된다.
단순회귀분석 - 선형 회귀
단순회귀분석은 선형회귀라고 하며 그 모양은 1차 함수인 y=ax+b의 형태를 가진다. 여기서 a를 가중치라고 한다.
데이터를 머신러닝할 때 중요한 점은 어떤 분석으로 접근할지 아는 것이다.
모델은 전처리한 데이터를 넣어 구하기 때문에 넣는 데이터에 대한 이해(도메인 지식)가 중요하다.
데이터 준비
먼저 csv파일을 불러오거나 sns.load_dataset('mpg')를 통해 데이터를 가져온다.
# 연비
import seaborn as sns
df = sns.load_dataset('mpg')여기선 seaborn의 자동차별 연비 데이터를 가져온다.
불러운 데이터가 어떤 것인지 탐색을 한다.
# 표로 확인
df.head() # 초반 행 확인
df.info() # 결측치, 자료형 확인
df.describe() # 값 분포 확인
df.isna().sum() # df.isnull().sum(), 결측치 개수 확인
df.duplicated().sum() # 중복값 확인
df['column_name'].unique() # 고유한 값 탐색
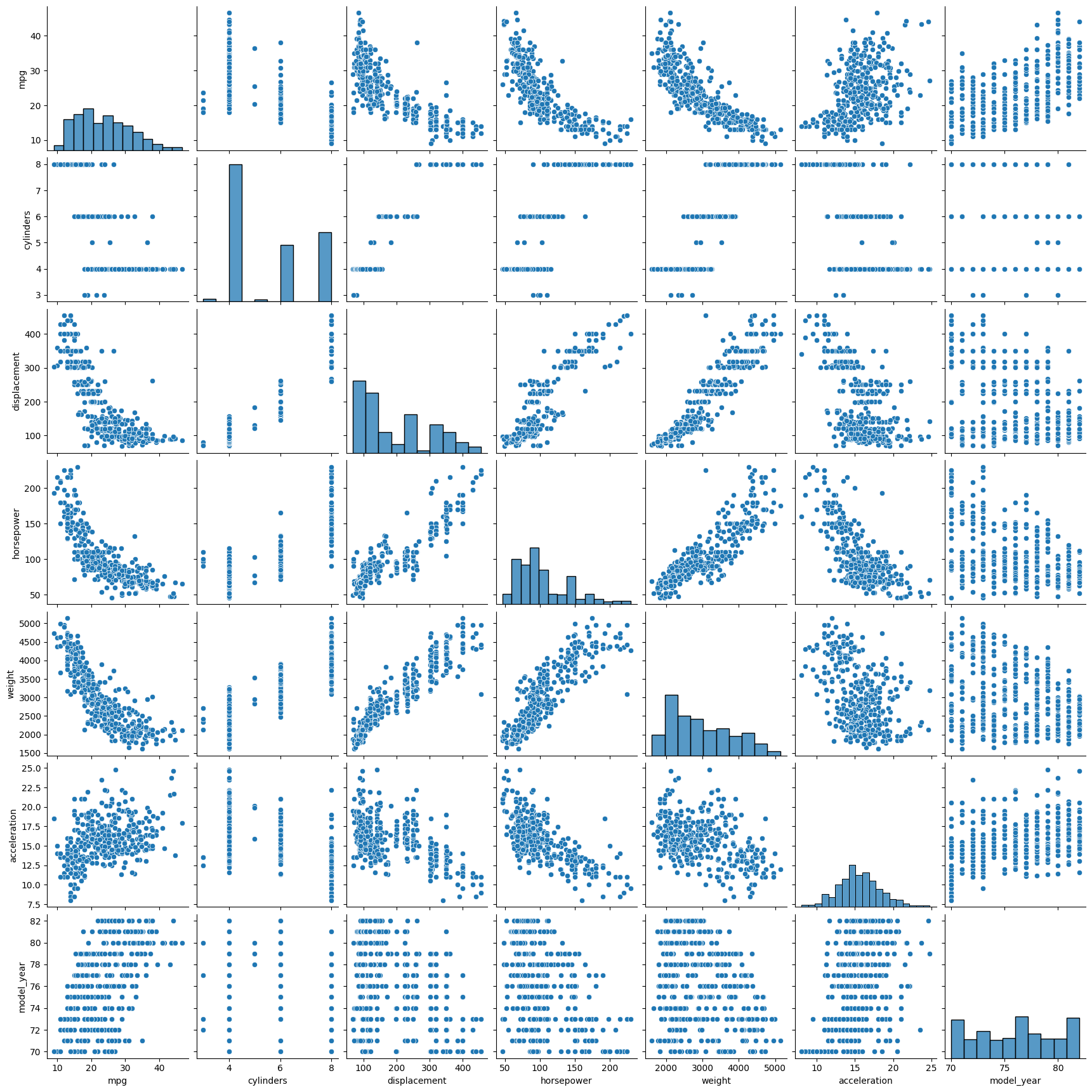
# 그래프로 확인
sns.pairplot(df) # 모든 관계를 seaborn의 pairplot()으로 확인
corr = df.corr(numeric_only=True) # 데이터 간 상관계수
sns.heatmap(corr, cmap='coolwarm', annot=True, cbar=True, square=True) # 시각화필요에 따라서 값을 제거하거나 변경, 또는 자료형을 변경한다.
# NaN 제거하기
df = df.dropna() # NaN 포함하는 행 삭제
df = df.reset_index(drop=True) # 인덱스 초기화, 기존 인덱스 삭제
df.isna().sum()
df['column_name'] = df['column_name'].replace('-',pd.na) # - 를 NaN으로 변경
df['column_name'] = df['column_name'].astype('float') # 자료형 변경탐색을 한 뒤 데이터 전처리 작업 전략을 세운다.
# 결측치 처리 : NA, NA와 같은 데이터들..... -1, '-', '?' 특수기호와 같이 의미없는 데이터
# 이상치 처리

sns.regplot(df, y='mpg', x='weight')
enumerate() 함수는 반복 가능한(iterable) 객체를 입력으로 받아, 각 요소와 해당 요소의 인덱스를 포함하는 열거형 객체를 반환합니다. 이 함수는 리스트, 튜플, 문자열 등 다양한 반복 가능한 객체에 사용할 수 있으며, 루프에서 인덱스와 값을 동시에 처리할 때 매우 유용합니다.
import matplotlib.pyplot as plt
plt.figure(figsize=(12,7))
for idx, col in enumerate(numeric_col.columns[1:]):
plt.subplot(2,3,idx+1)
sns.regplot(df2, y='mpg', x=col)
plt.show()
단순회귀분석 - 선형회귀
from sklearn.linear_model import LinearRegression
# sklearn 계열의 모델은 학습 순서 및 사용 메소드가 정해져 있음
# sklearn 계열 2차원 데이터를 원한다.
model = LinearRegression() # 기본 객체 생성
# 학습
model.fit(x_train, y_train)
# 평가 결정계수 이용해서 평가, 내부에서 예측도 같이 이루어진다.
# 결정계수는 1에 가까울수록 성능이 좋음
# 결정계수 : R^2 모델이 데이터의 변동성을 잘 설명하는지 나타내는 지표
# 1 - (SSR/SST)
# SSR : 잔차(Sum of Squares due to Regression) 정답-예측 차이의 제곱의 합
# SST : 실제값-평균값 제곱합(Total Sum of Squares)
score = model.score(x_test, y_test)
print(f'MSE의 값 : {score}') # 1에 가까울수록 좋음
# 예측
# y_predict = model.predict(x_test)# MSE
from sklearn.metrics import mean_squared_error
y_predict = model.predict(x_test)
mean_squared_error(y_test, y_predict) # 두 값의 오차예측값과 실제값 사이의 평균 제곱 오차(MSE)를 계산
선형회귀는 단순회귀라고도 하며 y = ax1 + bx2 = cx3 ....의 방정식을 구하는 것을 목표로 한다.
# 선형계수 : a,b,c, 입력 데이터 : x1, x2, x3
# y = w1x1 + w2x2 + w3x3 + b 를 푼다. w는 가중치라고 한다.
print(f'기울기 : {model.coef_} 절편 : {model.intercept_}')
# 기울기 : [-0.00610503 -0.03982949 -0.00529518] 절편 : 44.49785801830489
model.predict(x_test.iloc[[0]]) # 24.10158726
arr = x_test.iloc[0].values
-0.00610503*arr[0] -0.03982949*arr[1] -0.00529518*arr[2] + 44.49785801830489 # 24.10158116830489y_predict = model.predict(x_test)
sns.kdeplot(y_test, label = 'y')
sns.kdeplot(y_predict, label = 'y_predict')
plt.legend()
plt.show()plt.scatter(x_train,y_train)
# plt.scatter(x_test,y_test)
plt.scatter(x_test,model.predict(x_test))

다중회귀분석 - Polynomial
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(degree=2)
X_poly = poly.fit_transform(X)
x_train_poly, x_test_poly, y_train, y_test = train_test_split(X_poly,y,random_state=42)
plt.scatter(x_train, y_train)
plt.scatter(x_test, model.predict(x_test_poly))
y_predict = model.predict(x_test_poly)
sns.kdeplot(y_test)
sns.kdeplot(y_predict)
plt.show()

# 회귀
# 선형회귀(단항 다항) - 직선의 방정식
# 비선형회귀(다중회귀) 차수를 2차원 이상으로 올려서 학습
# 평가방법은 단순히 오차를 게산 ?? 이 값이 좋은지 나쁜지 모른다.
# 0 ~ 1의 사이의 값을 가지는 R-Square 결정계수.... 1에 가까울수록 높은 성능 model.score 함수를 이용
# 단순선형보다는 비선형(부드러운 곡선)형태가 모델을 잘 설명해 줄 수 있다.
# 연비측정
# 데이터 고정 -> 먼저 모델 최적화 -> 데이터 튜닝
# 모델선정
from sklearn.linear_model import LinearRegression
model = LinearRegression() # sklearn은 모델 적용방법이 다 같아 정의해주면 좋음
# 학습
model.fit(x_train, y_train)
# 평가 score 결정계수 R^2 0~1 1에 가까운 값이 best
# 시각적인 평가 밀도함수를 통해 차이를 본다
model.score(x_test, y_test)성능개선 - 라벨링, 스케일링
LabelEncoder
# df['origin'] 라벨링
# df['name'] 라벨링
# 범주형 데이터는 라벨링
from sklearn.preprocessing import LabelEncoder
test = ['a', 'b', 'a', 'c']
label = LabelEncoder()
label.fit_transform(test)범주형 데이터를 라벨링
StandardScaler() 적용
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
poly = PolynomialFeatures()
X_scaled_poly = poly.fit_transform(X_scaled)
x_train,x_test,y_train,y_test = train_test_split(X_scaled_poly,y,test_size=0.2,random_state=42)
model = LinearRegression()
model.fit(x_train,y_train)
model.score(x_test,y_test)StandardScaler는 데이터를 분포를 변형시키지 않으며 평균 0, 표준편차 1로 맞춤
다항식의 차수를 높이는 경우
# 차수를 높이면 학습용 데이터를 다 통과하려는 경향을 보이게 됨
# train한 값보다 test가 약간 낮아야 좋은 모델
# 학습 모델값만 너무 신뢰
# overfitting - 과적합
- 과적합을 피하려면?
- 학습데이터에 치우쳐져서(과도한 학습) 학습데이터의 성능은 좋지만 테스트 데이터는 낮은 성능 즉 둘 사이의 차이가 큰 경우
- 해결방안
- 쉽게 생각하면 위의 그래프에서 그래프를 살짝 펴준다고 생각
- 1. 학습 횟수를 줄인다. (여기서는 차수를 줄인다)
- 2. 데이터를 확보해서 충분히 많은 데이터를 학습에 적용한다. --> 현실적으로 불가능
- 과적합에 패널티 부여
- 최신모델 사용
- 최신기법 사용 - 앙상블
Gradient Boosting Regressor
model = GradientBoostingRegressor(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42)
model.fit(X_train, Y_train)Gradient Boosting은 각 단계에서 이전 모델의 오류(잔차)를 줄이기 위해 새로운 모델을 추가하는 방식으로 작동
- 초기 모델 생성: 초기 예측값을 제공하는 기본 모델을 학습합니다.
- 잔차 계산: 현재 모델의 예측값과 실제값 사이의 차이인 잔차를 계산합니다.
- 잔차 예측 모델 학습: 잔차를 예측하는 새로운 약한 학습자를 학습합니다.
- 모델 업데이트: 새로 학습된 모델을 기존 모델에 추가하여 전체 모델을 개선합니다.
- 반복: 위 과정을 여러 번 반복하여 점진적으로 모델 성능을 향상시킵니다
'프로그래밍 > SK AI 캠프' 카테고리의 다른 글
| 캠프 20일차 - 머신러닝(분류와 로지스틱 회귀) (0) | 2024.09.23 |
|---|---|
| SKN AI 캠프 4주차 (0) | 2024.09.19 |
| 캠프 18일차 - 데이터 시각화 (2) | 2024.09.12 |
| 캠프 17일차 - 데이터 전처리(2) (0) | 2024.09.12 |
| 캠프16일차 - 데이터 전처리(1) (0) | 2024.09.12 |



